La section précédente présentait un ensemble de métriques de modèle, toutes calculées à une seule valeur de seuil de classification. Toutefois, si vous souhaitez évaluer la qualité d'un modèle pour tous les seuils possibles, vous avez besoin d'outils différents.
Courbe ROC (Receiver Operating Characteristic)
La courbe ROC est une représentation visuelle des performances du modèle pour tous les seuils. La version longue du nom, "caractéristique de fonctionnement du récepteur", est un vestige de la détection radar de la Seconde Guerre mondiale.
La courbe ROC est tracée en calculant le taux de vrais positifs (TVP) et le taux de faux positifs (TFP) à chaque seuil possible (en pratique, à des intervalles sélectionnés), puis en représentant le TVP par rapport au TFP. Un modèle parfait, qui, à un certain seuil, présente un TPR de 1,0 et un FPR de 0,0, peut être représenté par un point en (0, 1) si tous les autres seuils sont ignorés, ou par les éléments suivants:

Aire sous la courbe (AUC)
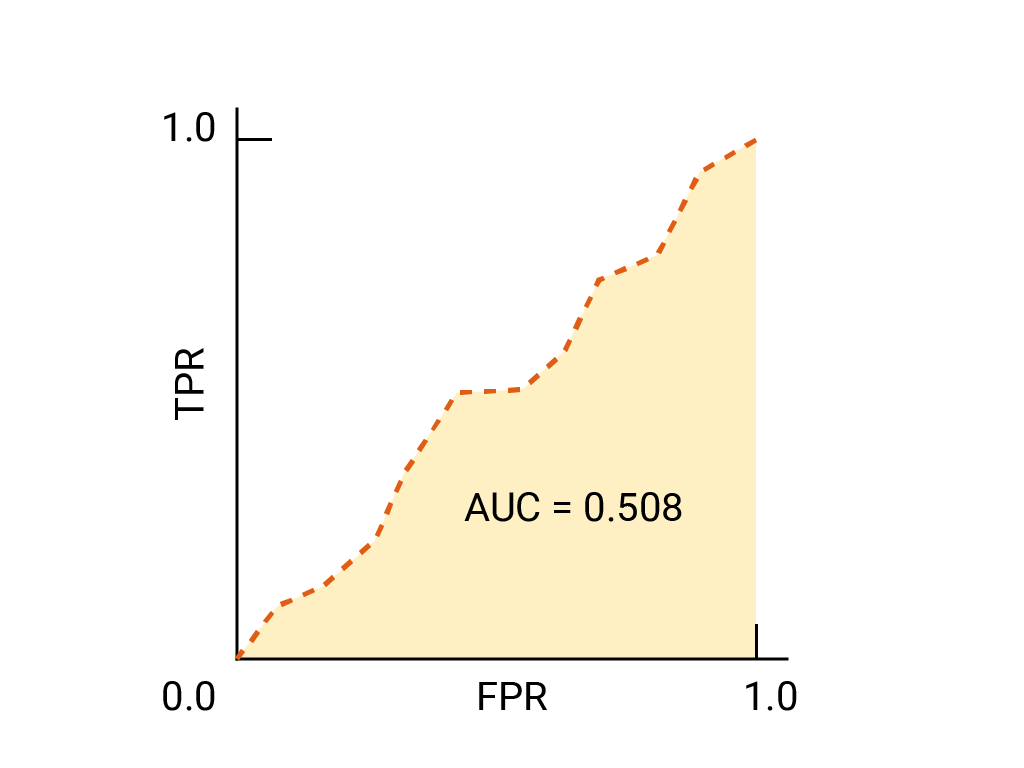
L'aire sous la courbe ROC (AUC) représente la probabilité que le modèle, s'il reçoit un exemple positif et un exemple négatif choisis aléatoirement, classe l'exemple positif plus haut que l'exemple négatif.
Le modèle parfait ci-dessus, qui contient un carré dont les côtés mesurent 1, a une aire sous la courbe (AUC) de 1,0. Cela signifie qu'il y a une probabilité de 100% que le modèle classe correctement un exemple positif choisi aléatoirement plus haut qu'un exemple négatif choisi aléatoirement. En d'autres termes, en examinant la répartition des points de données ci-dessous, l'AUC indique la probabilité que le modèle place un carré choisi au hasard à droite d'un cercle choisi au hasard, indépendamment de l'emplacement du seuil.

Plus concrètement, un classificateur de spam avec un AUC de 1,0 attribue toujours à un e-mail de spam aléatoire une probabilité plus élevée d'être du spam qu'un e-mail légitime aléatoire. La classification réelle de chaque e-mail dépend du seuil que vous choisissez.
Pour un classificateur binaire, un modèle qui fonctionne exactement aussi bien que les suppositions aléatoires ou les tirages de pièces de monnaie a un ROC qui est une ligne diagonale de (0,0) à (1,1). L'AUC est de 0,5, ce qui représente une probabilité de 50% de classer correctement un exemple positif et négatif au hasard.
Dans l'exemple du classificateur de spam, un classificateur de spam avec un AUC de 0,5 attribue une probabilité plus élevée d'être du spam à un e-mail de spam aléatoire qu'à un e-mail légitime aléatoire seulement la moitié du temps.

(Facultatif, avancé) Courbe de précision/rappel
L'AUC et le ROC sont utiles pour comparer des modèles lorsque l'ensemble de données est à peu près équilibré entre les classes. Lorsque l'ensemble de données est déséquilibré, les courbes de précision-récupération (PRC) et la zone sous ces courbes peuvent offrir une meilleure visualisation comparative des performances du modèle. Les courbes de précision/rappel sont créées en traçant la précision sur l'axe Y et le rappel sur l'axe X pour tous les seuils.

AUC et ROC pour choisir un modèle et un seuil
L'AUC est une mesure utile pour comparer les performances de deux modèles différents, à condition que l'ensemble de données soit à peu près équilibré. Le modèle ayant la plus grande surface sous la courbe est généralement le meilleur.


Les points d'une courbe ROC les plus proches de (0,1) représentent une plage des seuils les plus performants pour le modèle donné. Comme indiqué dans les sections Seuils, Matrice de confusion et Choix de la métrique et compromis, le seuil que vous choisissez dépend de la métrique la plus importante pour le cas d'utilisation spécifique. Prenons les points A, B et C du diagramme suivant, chacun représentant un seuil:

Si les faux positifs (fausses alarmes) sont très coûteux, il peut être judicieux de choisir un seuil qui donne un FPR plus faible, comme celui du point A, même si le TPR est réduit. À l'inverse, si les faux positifs sont peu coûteux et les faux négatifs (vrais positifs manqués) très coûteux, le seuil du point C, qui maximise le TPR, peut être préférable. Si les coûts sont à peu près équivalents, le point B peut offrir le meilleur équilibre entre le taux de conversion et le taux de faux positifs.
Voici la courbe ROC pour les données que nous avons vues précédemment:
Exercice: Vérifiez votre compréhension







(Facultatif, avancé) Question bonus
Imaginons une situation où il est préférable d'autoriser un certain nombre de spams à atteindre la boîte de réception plutôt que d'envoyer un e-mail essentiel à l'activité dans le dossier de spam. Vous avez entraîné un classificateur de spam pour cette situation, où la classe positive est le spam et la classe négative est le non-spam. Parmi les points suivants sur la courbe ROC de votre classificateur, lequel est préférable ?

